Es gibt verschiedenste Arten der rhythmischen Permutation von Motiven. Ich möchte mich hier auf Phrasierungsmöglichkeiten beschränken. Im Gegensatz zu Techniken wie Verdichten/Reduzieren oder Diminution/Augmentation, bleibt sowohl die Menge der Noten, als auch die Länge des Zeitraumes, in dem sie vorkommen, gleich. Lediglich die Länge der einzelnen Noten und damit ihr rhythmisches Verhältnis zueinander wird verändert.
Wenn man Erfahren im Umgang mit n-tolischen Phrasierungsmöglichkeiten ist, setzt man sie genau wie Staccato, Legato und Akzente intuitiv ein. Um diese Erfahrung zu sammeln, kann ein systematisches Gegenüberstellen und Kategorisieren hilfreich sein.
Gehen wir von einem einfachen, kurzen Motiv aus: zwei gleichwertige Schläge innerhalb einer Viertelnote -die Achtelnoten c' und a.

Mit „gleichwertig“ beschreibe ich die musikalische Relevanz der Noten. Das Motiv ist somit nicht reduzierbar, da beide Noten gleich wichtig für das Motiv sind. Ein Beispiel für nicht gleichwertige Schläge ist Abbildung 5, bei welcher der akzentuierte Schlag wichtiger als der darauf folgende und demnach nicht mit ihm gleichwertig ist.
Ein
gängiges Beispiel einer n-tolischen
Phrasierungsmöglichkeit, ist die triolische-
bzw. Shuffle-Version des Motivs:
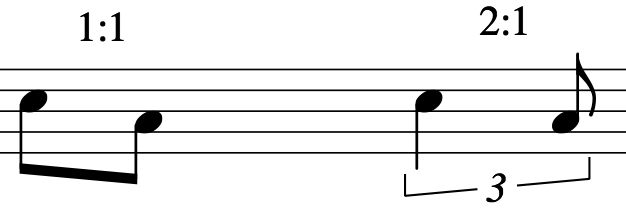
Das exakte rhythmische Verhältnis mehrerer Noten zueinander kann am einfachsten in ganzzahligen Verhältnissen dargestellt werden. Diese geben dem Erfahrenen schnell Aufschluss über den Charakter der Phrasierung.
Die
Noten stehen in ihrer Grundform im rhythmischen Verhältnis 1:1 zu
einander, da sie gleich lang sind. Eine Viertel und eine Achtelnote
stehen im Verhältnis 2:1 zueinander, da die Viertelnote doppelt
(also zweimal) so lang ist wie die Achtelnote (2 Achtel zu 1 Achtel
also 2:1) Eine Vierteltriole und eine achtel Triole ergeben eine
Viertelnote. Die beiden Noten stehen im Verhältnis 2:1 zueinander.
(2 Achteltriolen zu 1 Achteltriole also 2:1)
Es gibt unendlich viele Phrasierungsmöglichkeiten, wovon jedoch nur wenige praktikabel sind. Um einen sinnvollen Überblick über diese zu bekommen, kann man sich ein Komplexitätslimit setzten und davon ausgehend alle möglichen Phrasierungen auflisten.
Ein solches Limit könnte sein, keine kleinere Subdivision als 32stel-9-Tolen zu verwenden.
Listet man nun alle sinnvollen Paare aus jeder möglichen Subdivision (also 9-Tolen, 32stel, Septolen, Sextolen, Quintolen, 16tel, Triolen und Achtel) auf, kommt man auf die möglichen Paare: 5:4, 5:3, 4:3, 5:1, 3:2, 3:1, 2:1, 1:1.

Hört
man sich alle Phrasierungsmöglichkeiten an, wird man vermutlich
folgendes daraus schließen: Während die 9-Tolen und Septolen sich
wie eine geswingte Version des Originals anhören, wirken die 32stel,
Quintolen und Triolen bereits wie ein kurz-lang-Shuffle. Die Sextolen
und die 16tel haben, aufgrund ihres Verhältnisses, bei dem einer der
Schläge mehr als doppelt so lang ist wie der andere x
: y < (x/2), bereits einen stark veränderten Charakter,
der kaum als zwei gleichwertige Schläge gedeutet werden kann.
Möchte man das verhindern, bleiben die Phrasierungsmöglichkeiten: 5:4, 5:3, 4:3, 3:2, und 2:1.

Jedes ungleiche Paar kann man auf zwei Arten anordnen. Der Grund, warum 32stel (4:4), Sextolen (3:3) und 16tel (2:2), nicht zur Debatte stehen, ist weil sie äquivalent zu den Achtelnoten sind. 9-Tolen (6:3) und Sextolen (4:2) entsprechen den Achteltriolen. Welche Phrasierung für den musikalischen Kontext am besten ist, bleibt eine rein subjektive Entscheidung.
Im nächsten Beispiel kommen drei gleichwertige Schläge innerhalb einer Viertelnote vor: die Achteltriolen e', c' und a.
Ich habe nur Phrasierungsmöglichkeiten ausgewählt, die x : y ≥ (x/2) entsprechen.

9-Tolen
(3:3:3) und Sextolen (2:2:2) entsprechen Achteltriolen und 32stel
(2:4:2) entsprechen 16tel. 9-Tolen (2:5:2) entsprechen x
: y < (x/2) und sind als Repräsentation gleichwertiger
Strukturmitglieder ungeeignet. Achtel haben weniger als drei
Glieder und sind daher ebenfalls ungeeignet.
Das nächste Beispiel zeigt zwei 16tel Motive, ebenfalls mit e', c' und a. Die Strukturen beinhalten zwei gleichlange kurze Glieder und ein langes Glied (2:1:1 und 1:2:1).

Da
die beiden kurzen Glieder gleich lang, jedoch kürzer als das lange
Glied sein müssen, gibt es nur eine möglich Entsprechung pro
n-tolischer Permutation. Achteltriolen scheiden trotz ihrer drei
Glieder aus, da diese gleich lang sind. 32Stel (6:1:1) und Sextolen
(4:1:1) weichen schon sehr stark vom Motiv ab und werden daher in
Abbildung 4 nicht berücksichtigt.
Das
letzte Beispiel beinhaltet vier 16tel Noten: e', d', c', und a. In
diesem Fall wurde ein Akzent auf dem dritten Schlag gesetzt, welcher
darauf hindeutet, dass der dritte Schlag ein langes Glied sein
sollte. Hier spricht man nicht mehr von vier gleichwertigen Schlägen,
sondern von einem starken und drei schwachen Schlägen.

Da es in 9-Tolen und Quintolen nur ein langes Glied gibt, ist nur eine Entsprechung möglich. Bei Septolen gibt es drei lange Glieder und Sextolen haben zwei lange Glieder, daher gibt es jeweils drei Entsprechungen.
In Abbildung 5 habe ich bei den Sextolen und Septolen jeweils die Entsprechung gewählt, die ein kurzes vor dem betonten langen Glied hat, um den Akzent zu verdeutlichen.
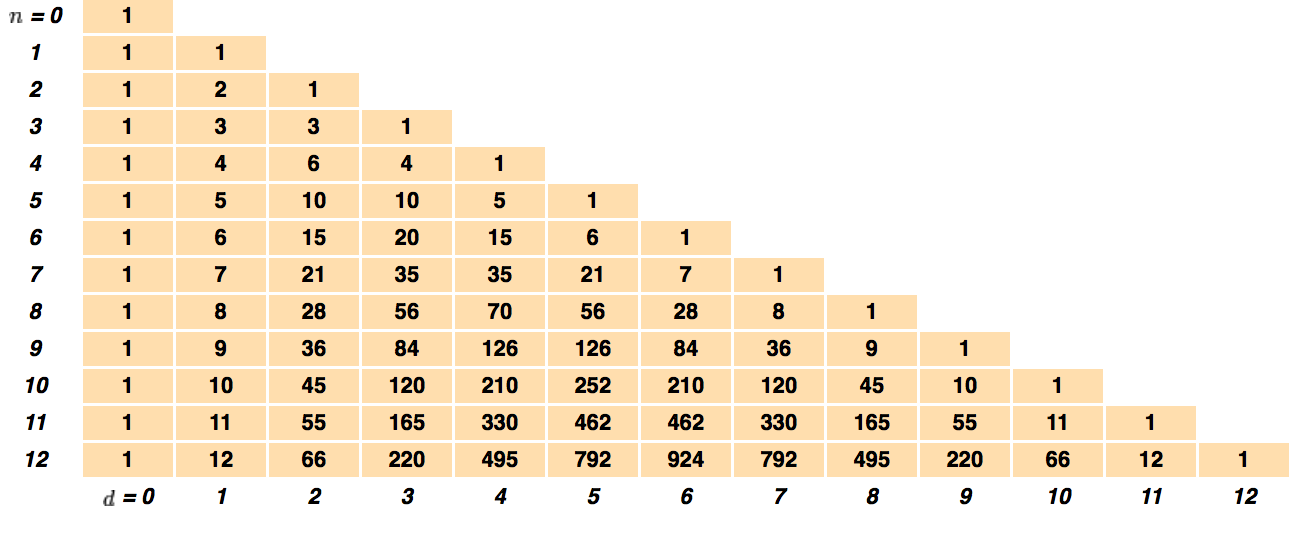
Anordnungsmöglichkeiten anhand des Pascalschen Dreiecks
Wie
man sieht, gibt es bei jeder Permutation von gleichwertigen Schlägen
genauso viele Anordnungsmöglichkeiten wie es rhythmische
Strukturmitglieder (Schläge/Noten) in der Phrase gibt. Das gilt
allerdings nur, wenn es zweigliedrige Rhythmen mit der Struktur x +
ny sind. Also zum Beispiel ein kurzes Glied und beliebig viele
lange Glieder (z.B 3:3:2:3 = lang:lang:kurz:lang).
Folgt ein zweigliedriger Rhythmus der Formel 2x + ny
(also z.B. 2x + 3y = 2kurz + 3lang = 3:2:2:3:3 = lang:kurz:kurz:lang:lang), so steigen die Anordnungsmöglichkeiten mit der Erhöhung von n in der Sequenz der Dreieckszahlen:
2x + 2y = 6 Anordnungsmöglichkeiten,
das oben genannte Beispiel 2x + 3y = 10 Anordnungsmöglichkeiten,
2x + 4y = 15 Anordnungsmöglichkeiten,
2x
+ 5y = 21 Anordnungsmöglichkeiten und so weiter. Die nächsten
Dreieckszahlen lauten 28, 36, 45, 55, 66, 78, 91, 105, 120,
136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435,
465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946,
990, 1035, 1081, 1128, 1176, 1225...
Folgt ein zweigliedriger Rhythmus der Formel 3x + ny, steigen die Anordnungsmöglichkeiten mit der Erhöhung von n in der Sequenz der Tetraeder-Zahlen:
3x + 2y = 10 Anordnungsmöglichkeiten,
3x + 3y = 20 Anordnungsmöglichkeiten,
3x + 4y = 35 Anordnungsmöglichkeiten,
3x
+ 5y = 56 Anordnungsmöglichkeiten und so weiter. Die nächsten
Tetraederzahlen lauten 84, 120, 165, 220, 286, 364, 455, 560,
680, 816, 969, 1140, 1330, 1540, 1771, 2024, 2300, 2600, 2925, 3276,
3654, 4060, 4495, 4960, 5456, 5984, 6545, 7140, 7770, 8436, 9139,
9880, 10660, 11480, 12341...
Folgt ein zweigliedriger Rhythmus der Formel 4x + ny,
steigen
die Anordnungsmöglichkeiten mit der Erhöhung von n in
der Sequenz der Pentachoron-Zahlen: 1, 5, 15, 35, 70, 126,
210, 330, 495, 715, 1001, 1365, 1820, 2380, 3060, 3876, 4845, 5985,
7315...
Die
sich ergebenden Zahlenreihen beschreiben die Menge an physischen
Bausteinen die es braucht, um ein gleichseitiges Dreieck zu
konstruieren. Jede Erhöhung von x fügt eine neue Dimension hinzu.
Während 2x ein zweidimensionales gleichseitiges Dreieck bildet,
bilden 3x und 4x drei- und vierdimensionale Formen, die aus
gleichseitigen Dreiecken gebildet werden: Tetraeder
und Pentachorone.
Folgt ein zweigliedriger Rhythmus der Formel nx + ny, (wobei n den gleichen Wert bei beiden hat) steigen die Anordnungsmöglichkeiten mit der Erhöhung von n in der Sequenz der mittleren Binomialkoeffizienz:
2x + 2y = 6 Anordnungsmöglichkeiten,
3x + 3y = 20 Anordnungsmöglichkeiten,
4x + 4y = 70 Anordnungsmöglichkeiten,
5x
+ 5y = 252 Anordnungsmöglichkeiten und so weiter. Die nächsten
Zahlen der mittleren Binomialkoeffizienz lauten: 924, 3432,
12870, 48620, 184756, 705432, 2704156, 10400600, 40116600, 155117520,
601080390, 2333606220, 9075135300, 35345263800, 137846528820,
538257874440, 2104098963720, 8233430727600, 32247603683100...
Das Muster, welches man in diesen Zahlen erkennen kann, ist das des pascalschen Dreiecks. Das pascalsche Dreieck ist eine geometrische Anordnung rekursiv produzierter Zahlen, die die Binomialkoeffizienz generieren.
Damit können die Anordnungs-möglichkeiten jeder Kurz-Lang Kombination errechnet werden und damit jede mögliche Variation in Betracht gezogen werden.
N-tolische Phrasierungsmöglichkeiten einer Melodie
Zum Abschluss möchte ich die mögliche Anwendung dieser Phrasierungsmöglichkeiten anhand einer viertaktigen Beispielmelodie zeigen. Sie besteht aus drei Motiven, also melodischen Phrasen. Zuerst wird die Melodie in ihrer simplen Grundform gezeigt. Als nächstes wird sie im quintolischen Quantisierungsraster phrasiert. In der dritten Zeile wird die Melodie im septolischen Quantisierungsraster phrasiert und in der vierten Zeile wird eine gemischte Phrasierung aus beinahe allen behandelten Subdivisionen gezeigt.

In jeder dieser Variationen ist die Melodie unweigerlich wiederzuerkennen. Jede Phrase weist jedoch in jeder Version einen eigenständigen Charakter auf. Diese drei alternativen Versionen sind natürlich nur drei von unüberschaubar vielen.
Die exakt ausnotierte Phrasierung kann eine Partitur der Vorstellung des Komponisten ein stückweit näher bringen oder durch kreatives Experimentieren eine simple Idee in ein neues Licht rücken. Es ist allerdings immer wichtig die ausführenden Musiker einschätzen zu können. Die meisten Instrumentalisten und Sänger, die keine komplexen zeitgenössischen Stücke gewohnt sind, fänden zum Beispiel 9-Tolen eher abschreckend.
Eine weitere Veranschaulichung anhand eines bekannten Weihnachtsliedes:

Kurz-Lang-Rhythmus Paare
Das einfachste rhythmische Verhältnis, abgesehen von 1:1, ist kurz zu lang. Dieses Verhältnis kann von der Auslegung des Künstlers abhängig sein, wie es im Swing erwünscht ist, oder in konkreten Zahlenverhältnissen ausdrückbar sein. Diese Paare können die Basis für verschiedenste Rhythmen sein, zum Beispiel 3+3+2 (lang+lang+kurz). Bei schnellem Tempo, bei dem das Zählen der einzelnen Schläge nicht mehr möglich ist, muss der Interpret die Längenverhältnisse der Gruppen kennen und in Kurz-Lang-Einheiten denken. Ein Beispiel dafür sind schnelle 9/8 (2+2+2+3) Takte in serbischer Zigeunermusik.
Fibonacci-Reihe als Basis für das Verhältnis in Kurz-Lang-Rhythmus Paaren
Die Fibonacci-Zahlenreihe ist eine mathematische Sequenz, deren aufeinanderfolgende Zahlenpaare im Verhältnis zueinander sich nach und nach dem Golden Schnitt Phi (1.618033988749894848) annähern. Sie wird gebildet durch die Addition der aufeinanderfolgenden Zahlenpaare, beginnend mit Null, Eins, Eins und Zwei. Also 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 und so weiter. Die unendliche Zahlenreihe, die sich ergibt, beginnt demnach 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811.
Fibonacci-Zahlen ist auch in der Natur in unterschiedlichsten Formen zu finden. Das ästhetische und vor allem ähnliche Verhältnis zwischen den aufeinanderfolgenden Zahlen, macht die Reihe zur perfekten Quelle für austauschbare Kurz-Lang-Rhythmus-Paare.
So kann man zum Beispiel 2+1 (lang+kurz) durch 3+2 , 5+3, 8+5 oder 13+8 ersetzen.
Die rhythmische Sequenz 3+3+2 lässt sich durch 5+5+3 und 8+8+5 ersetzen. Behält man das Tempo der zwei langen Glieder bei, erhält man eine komplexe rhythmische Permutation, bei Beibehaltung der zugrundeliegenden Struktur und Klangästhetik.
Es kling wage ausgedrückt ähnlich, und doch anders.
In Abbildung 7 wird diese Idee in zwei Takten aus Billie Jean von Michael Jackson umgesetzt. Die eintaktige Bassfigur füllt die lang+lang+kurz Sequenz mit 3+3+2 Strukturgliedern aus, die in ihrer Grundform (Bsp.1) gleich lang sind.
Die Melodie des Themas unterteilt die langen Glieder (Dreiergruppen) wiederum in lang+kurz und kurz+lang Paare (2+1 und 1+2). So kann die Melodie als (2+1)+(1+2)+2 und folglich als (3+2)+(2+3)+3 in Bsp.2, und (5+3)+(3+5)+5 in Bsp.3 betrachtet werden.

Da die Länge der langen Glieder gleich bleibt (73 bpm), und das Verhältnis zwischen den Kurz-Lang-Gruppen so ähnlich ist, wirkt es fast wie eine Überlagerungen über die Grundform, wie sie im Notenbeispiel der Abbildung 8 gezeigt wird. Jedoch klingt die Fibonacci-Kurz-Lang-Sequenz etwas homogener aufgrund der gleichbleibenden Subdivision. Aus dem gleichen Grunde ist sie auch für Musiker bedeutend einfacher zu visualisieren und umzusetzen.

Da in der Grundform (Bsp.1) alle Schläge der Bassfigur gleichwertig sind, sind die Anordnungsmöglichkeiten innerhalb der permutierten Glieder nach Belieben auskostbar.
Zum Beispiel sind im ersten Takt des Bsp.2 der Abbildung 7 die drei Strukturmitglieder der langen Gruppen in (2+1+2)+(2+1+2) gegliedert, während sie im zweiten Takt in (2+1+2)+(1+2+2) gegliedert sind. Solche subtilen Variationen bringen Leben in ein Arrangement. Ähnliches ist in den Takten von Bsp.3 zu vernehmen: (3+2+3)+(3+2+3)+(3+2) und (3+3+2)+(2+3+3)+(2+3).
Eine effiziente Möglichkeit der Notation ohne ständigen Tempowechsel, kann durch n-tolische Taktarten verwirklicht werden. In Abbildung 9 wurde das lange Glied als Viertelnote deklariert. Die Subdivisionen sind nun auf die Viertelnote bezogen.

2/12 bedeutet, dass zwei Achteltriolen in diesem Takt sind. Da in eine ganze Note zwölf Achteltriolen passen, bezeichnet man sie auch als Zwölftel. 3/20 bedeutet, dass drei 16telquintolen in diesem Takt sind. Da in eine ganze Note zwanzig 16telquintolen passen, bezeichnet man sie auch als Zwanzigstel.
Auf diese Weise kann man simplen Rhythmen eine neue Dimension verleihen. Der US-amerikanische Pianist Vijay Iyer ist bekannt für seine rhythmisch anspruchsvollen Kompositionen und Arrangements. Er hat dieses Prinzip bei seinen Piano-Trio Arrangements von Mystic Brew (Ronnie Foster) und Human Nature (Michael Jackson) angewandt.
Ich würde als Hörbeispiel Mystic Brew (Trixation Version), welches der achte Titel auf Vijay Iyers Album Historicity (ACT, 2009) ist, empfehlen. Hört man dem Piano zu, sind die Wechsel der Subdivisionen sehr klar wahrnehmbar.
Als Hilfestellung liste ich hier alle Subdivisionen mit dem Zeitraum ihres Auftretens auf:
0:00 bis 1:06 – 3+3+2
1:07 bis 1:30 – 5+5+3
1:31 bis 2:45 – 8+8+5
2:46 bis 3:15 – 3+3+2
3:16 bis 3:39 – 5+5+3
3:40 bis 4:24 – 8+8+5
und ab 4:25 wieder – 3+3+2 bis zum Schluss.
Eine konsequente Weiterführung dieser Idee in Verbindung mit Überlagerungen wie in der Abbildung 8, wäre das Pseudo-Accelerando in meiner Komposition Indignation aus der Jazz-Suite Twenty-Eight Moments 'till Spring. Zahlenpaare aus der Fibonacci- und der verwandten Lucas-Zahlenreihe werden in verdichtender Anordnung als Überlagerungen über die Sequenz 2+2+3/4 über einer statischen (2/4)+(3+3/8) – Bassfigur gesetzt. Die Zahlenpaare sind (3:2)+(5:3), 4+6, (5:4)+(8:6), 6+9, (7:4)+(11:6) und 8+12. Der Effekt ist ein stetiges Schnellerwerden bei jedem Subdivisions-Wechsel.

