Dsilton presentation 2016/2017

Error and timbre:

The error of a physically vibrating instrument must be considered when working with microtonal intervals smaller than a quarter-tone. For instance, the electric guitar has an error caused by the amplitude of the string. An open string played fortissimo is up to 20c sharp at the beginning of note and only within about a second reaches its target pitch. And even the best guitars are, of course, prone to become out of tune due to change in humidity or temperature or during intense passages in a piece. A deviation, which can lie anywhere between less than 1c and 10c per string.

But how pure or “in tune” an interval sounds to the ear is also heavily dependent on the timbre of the used instruments, as William A. Sethares demonstrated rather impressively in his book called Tuning, Timbre, Sepctrum, Scale, wherein he asked: „What is the relationship between the timbre of a sound and the intervals, scale, or tuning in which the sound appears in tune?“ He created an interesting comparison with an octave and a pseudo-octave, both played with a sound of bell-like timbre. While the real 2:1 octave was perceived as dissonant, the pseudo-octave with the ratio 2,1:1 sounded consonant – octave like. Now, stringed instruments are far less problematic, but with larger intervals, like for instance a double-octave, they do have the tendency to resonate “more in tune” with a slightly sharp double-octave.

So the physical limits of tuning-stability, the relation of timbre and tuning and the octave, in which an interval resonates, have to be considered when working with real instruments or sounds with complex timbres in microtonal space.

Serialism:

Oftentimes I start composing using some kind of serialism or strict concept.This might concern the rhythmic structure, the harmony and most often the melody. It makes creating and, most importantly, finishing a part easier for me by narrowing down the possibilities from unlimited to only a few, without breaking concept. The composing-process becomes more like a puzzle-solving experience that is about finding the most beautiful and creative way to solve it. Although I'm definitely guilty of breaking concept for, for instance, a more musically appealing note choice, or for a more practical guitar-fingering, that sounds just as good. The most obvious kind of serialism that can be found in my pieces is the use of tone-rows to create melodies and harmonic structures.

In a recent piece of mine, I used a 31 note tone-row. In the beginning of the piece it is vertically arranged in groups to form the chords of a ballad. After that it serves as melody and then, in its inversion, as a bass part.

The tone-row treats the 31 notes as equally spaced pitches, with every note having the same relevance. However, the relationship between the notes of a chord, I always view as approximations of whole number ratios.

For instance the third chord of Malend in Neon:

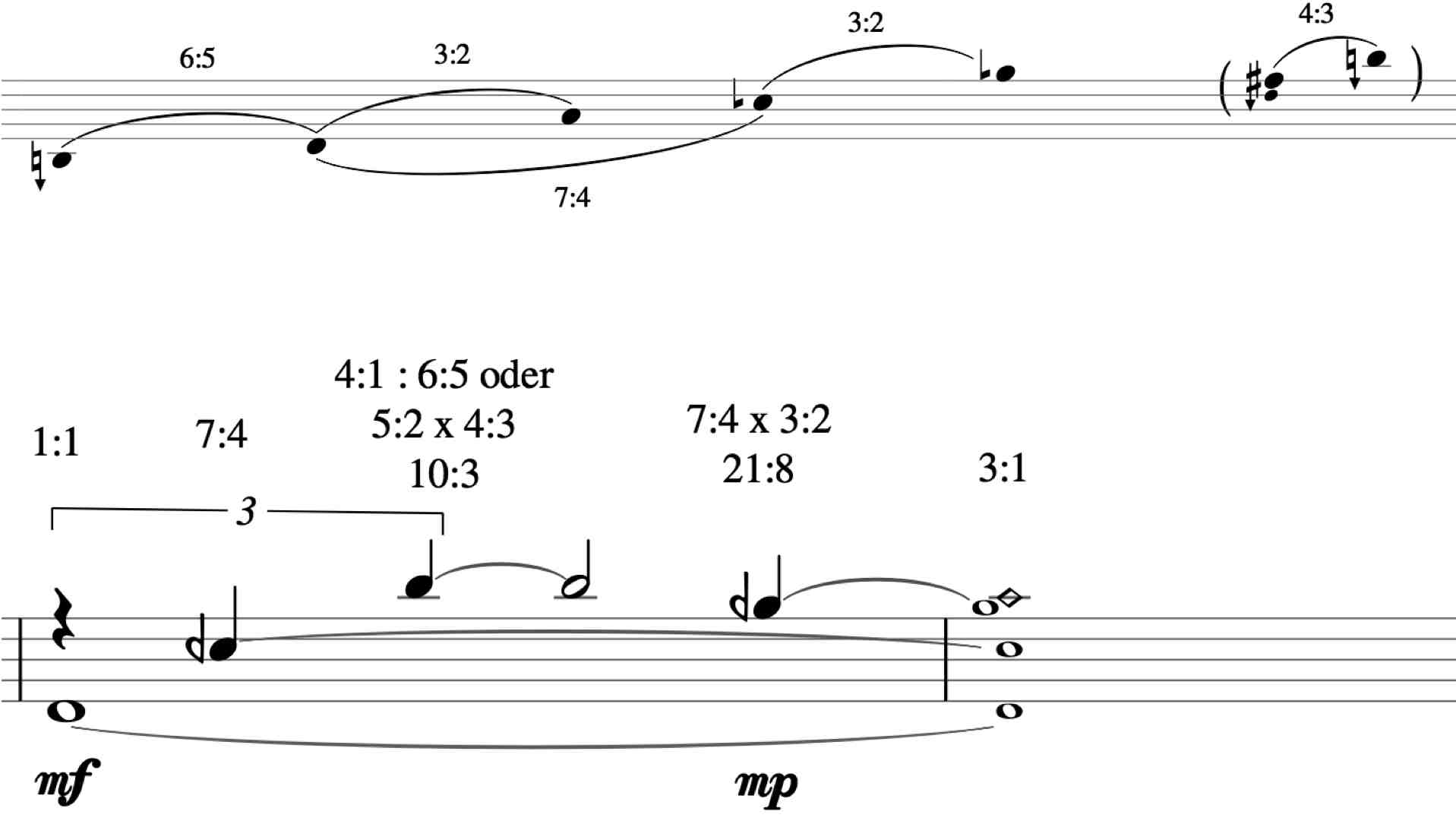
It has D as its fundamental.

7^th partial – a Cd, which is almost perfectly approximated in 31-ET (with about 1c error).

Major 6^th - B 10:3 - that is 8:3 * 5:4, which is the way I visualize it.

Pseudo 4^th - Gd with the ratio 21:8, which is the perfect fifth (3:2) of the 7^th partial. This one can be tuned justly by bending the string to pitch.

The perfect 5^th of the fundamental 3:2, which is about 5c flat in 31-ET.

That way, all of our music, rhythm and harmony alike, can be expressed in whole number ratios – in some cases though, we talk about approximations.

31-ET notation:

You might have noticed the use of quarter-tone accidentals in the chart.  For me it was important, that the notation represents the harmonic function a note has in my head.

So for instance, the 7^th partial can be notated as an augmented 6^th in 31-ET by using standard notation only. But to my ears, the 7^th partial in most situations has the tonal function and feel of a rather flat minor-7^th of a scale in the half-tone whole-tone-system. Therefore I started to use quarter-tone accidentals in addition to standard notation to depict notes as different intonations of a scale degree.

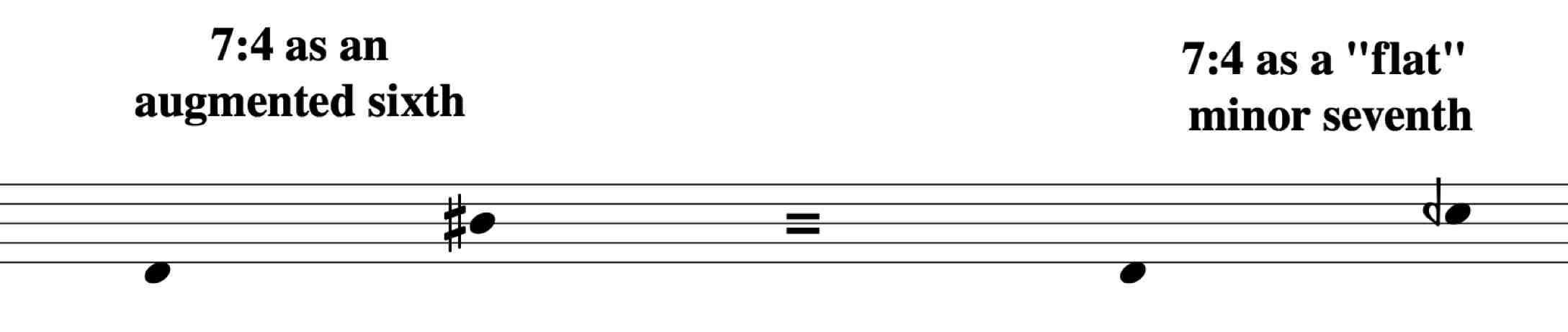
In this case a flat minor-7^th: C half-flat to D, instead of an augmented 6^th, B# to D.

Prismaschatten:

Another piece of mine called Prismaschatten uses a 7-limit 12 tone-row, which was derived from a melody I wrote that later formed the C-Section of the piece.  The intervals of the row are related to each other in simple 7-limit whole number ratios.

I also tried to keep the intervals rather simple in relation to the fundamental, which was the tuning note a, so they can be easily generated while practicing. The original piece was a string quartet called Schatten der Prismen, which translates to Shadow of Prisms. It was written completely in just intonation.

The notation-system I created to write in just intonation was highly influenced by The Extended Helmholtz-Ellis JI Pitch Notation and Ben Johnston's way of notating just intonation. It is based on standard notation but the scale that can be expressed by the standard accidentals is the endless Pythagorean scale, which is generated by stacking perfect-fifths with the ratio 3:2. To notate intervals based on prime-numbers other then 2 and 3, for instance 5:4 or 11:7, additional accidentals are used, which divide or multiply by different commas.

I liked the syntonic comma idea with the arrows attached to the enharmonic accidentals of the Helmholtz-Ellis JI Pitch Notation and also the septimal half-arrow, which somewhat looks like a seven but I couldn’t memorize the rest of them. So I used Ben Johnston's idea to use the prime numbers themselves as accidentals and made my own version that minimized, what I thought, were flaws of his notation. For instance, he inverted the numbers when the pitch was lowered. But an inverted 31 looked suspiciously like a 13. I just attached arrows to the numbers instead of inverting them, which works better in my opinion.

So I arranged the piece for our duo. We actually learned most of the piece from a chart I made with the original just-intonation notation, because I just copied, pasted and transposed from the string-quartet chart and we just looked for the closest approximation. I translated it into 31-ET notation afterwards.

It starts with the original tone-row in the keyboard-part of the Intro, followed by its inversion in A and B, which is thrown from instrument to instrument. It comes as a melody, a bass-part and even as a counterpoint. This is followed by section C with the original row as a melody.

The guitar-solo is over the original tone-row and the keyboard-solo is over the inversion of the row, like in part A. Both times it comes as a bass-part. After the Solos there is a section where the row and its inversion are played simultaneously, with slightly altered intonation, to fit each others tuning. This is followed by a reprise of part B and of the intro to wrap the piece up.

Instrument adaptation:

As there were a lot of different pitches, adapting the piece for the keyboards required more than one keyboard and technically rather challenging synthesizer work for Georg, where he uses key touch-response, in other words dynamics, to alter a pitch by a diminished second. Also the tremolos and glissandi, easy on stringed instrument, became precisely notated lines with complex subdivisions, which Georg arranged himself.

My notation:

Georg Vogels interpretation:

Georg wrote a Text about making pieces of mine work on his keyboards, which can be found on his website.

The 31-tone electric guitar part was easier to adapt because it is also a stringed instrument and has all the required notes available. I took most the viola- and 2^nd violin parts, which where mostly in its range, while the keyboards got the first violin and cello parts.

Adsunt Aves:

Now, as key-touch-response-intonation is a very time-consuming method, I tried to write a piece using only the detuned rhodes piano and guitar. This was, of course, a strict limitation concerning the available pitches and harmonies.

The piece is called Adsunt Aves – an arrangement of the German children's-song Alle Vöglein sind schon da. First I transformed the melody into a 12-tone-row. To fit the possible harmonies on the rhodes-piano, which has a fixed tuning, I took the liberty to alter every pitch by a diminished second, if necessary.

To make it more interesting rhythmically, I used the Fibonacci and Lucas sequence to morph the rhythms trough. This works great because every successive pair of numbers has a relation that converges towards phi. In other words, the proportions of the lengths of the notes stays about the same but the subdivision gets denser. 

For example the first bar in the original has four notes with 3, 1, 2 and 2 beats value, in this case: 8^th notes. If we morph this through the Fibonacci sequence and go one step higher, then 3 becomes 5, 1 becomes 2 and 2 becomes 3. In the second bar, I used the Lucas-numbers: so 3 becomes 4, 1 becomes 2 and 4 becomes 7.

I also used rhythmical modulations to have a wide pallet of different tempos. This can be found in almost all of the pieces in Dsiltons repertoire. For instance in the first version of the melody, it modulates gradually from very fast to very slow and then back at once into the original tempo from the beginning for the 2^nd version of the melody. I also used consecutive numerators in the time signatures. They start at the 4^th bar: 13,12, 11, 10, 9, 8, 7, 6... This makes the composing-process a fun challenge.